Quick start#
Welcome to Flax!
Flax is an open source Python neural network library built on top of JAX. This tutorial demonstrates how to construct a simple convolutional neural network (CNN) using the Flax Linen API and train the network for image classification on the MNIST dataset.
1. Install Flax#
!pip install -q flax>=0.7.5
2. Loading data#
Flax can use any data-loading pipeline and this example demonstrates how to utilize TFDS. Define a function that loads and prepares the MNIST dataset and converts the samples to floating-point numbers.
import tensorflow_datasets as tfds # TFDS for MNIST
import tensorflow as tf # TensorFlow operations
def get_datasets(num_epochs, batch_size):
"""Load MNIST train and test datasets into memory."""
train_ds = tfds.load('mnist', split='train')
test_ds = tfds.load('mnist', split='test')
train_ds = train_ds.map(lambda sample: {'image': tf.cast(sample['image'],
tf.float32) / 255.,
'label': sample['label']}) # normalize train set
test_ds = test_ds.map(lambda sample: {'image': tf.cast(sample['image'],
tf.float32) / 255.,
'label': sample['label']}) # normalize test set
train_ds = train_ds.repeat(num_epochs).shuffle(1024) # create shuffled dataset by allocating a buffer size of 1024 to randomly draw elements from
train_ds = train_ds.batch(batch_size, drop_remainder=True).prefetch(1) # group into batches of batch_size and skip incomplete batch, prefetch the next sample to improve latency
test_ds = test_ds.shuffle(1024) # create shuffled dataset by allocating a buffer size of 1024 to randomly draw elements from
test_ds = test_ds.batch(batch_size, drop_remainder=True).prefetch(1) # group into batches of batch_size and skip incomplete batch, prefetch the next sample to improve latency
return train_ds, test_ds
3. Define network#
Create a convolutional neural network with the Linen API by subclassing
Flax Module.
Because the architecture in this example is relatively simple—you’re just
stacking layers—you can define the inlined submodules directly within the
__call__ method and wrap it with the
@compact
decorator. To learn more about the Flax Linen @compact decorator, refer to the setup vs compact guide.
from flax import linen as nn # Linen API
class CNN(nn.Module):
"""A simple CNN model."""
@nn.compact
def __call__(self, x):
x = nn.Conv(features=32, kernel_size=(3, 3))(x)
x = nn.relu(x)
x = nn.avg_pool(x, window_shape=(2, 2), strides=(2, 2))
x = nn.Conv(features=64, kernel_size=(3, 3))(x)
x = nn.relu(x)
x = nn.avg_pool(x, window_shape=(2, 2), strides=(2, 2))
x = x.reshape((x.shape[0], -1)) # flatten
x = nn.Dense(features=256)(x)
x = nn.relu(x)
x = nn.Dense(features=10)(x)
return x
View model layers#
Create an instance of the Flax Module and use the Module.tabulate method to visualize a table of the model layers by passing an RNG key and template image input.
import jax
import jax.numpy as jnp # JAX NumPy
cnn = CNN()
print(cnn.tabulate(jax.random.key(0), jnp.ones((1, 28, 28, 1)),
compute_flops=True, compute_vjp_flops=True))
CNN Summary
┏━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━━┓
┃ path ┃ module ┃ inputs ┃ outputs ┃ flops ┃ vjp_flops ┃ params ┃
┡━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━━┩
│ │ CNN │ float32[1… │ float32[… │ 8708106 │ 26957556 │ │
├─────────┼────────┼────────────┼───────────┼─────────┼───────────┼────────────┤
│ Conv_0 │ Conv │ float32[1… │ float32[… │ 455424 │ 1341472 │ bias: │
│ │ │ │ │ │ │ float32[3… │
│ │ │ │ │ │ │ kernel: │
│ │ │ │ │ │ │ float32[3… │
│ │ │ │ │ │ │ │
│ │ │ │ │ │ │ 320 (1.3 │
│ │ │ │ │ │ │ KB) │
├─────────┼────────┼────────────┼───────────┼─────────┼───────────┼────────────┤
│ Conv_1 │ Conv │ float32[1… │ float32[… │ 6566144 │ 19704320 │ bias: │
│ │ │ │ │ │ │ float32[6… │
│ │ │ │ │ │ │ kernel: │
│ │ │ │ │ │ │ float32[3… │
│ │ │ │ │ │ │ │
│ │ │ │ │ │ │ 18,496 │
│ │ │ │ │ │ │ (74.0 KB) │
├─────────┼────────┼────────────┼───────────┼─────────┼───────────┼────────────┤
│ Dense_0 │ Dense │ float32[1… │ float32[… │ 1605888 │ 5620224 │ bias: │
│ │ │ │ │ │ │ float32[2… │
│ │ │ │ │ │ │ kernel: │
│ │ │ │ │ │ │ float32[3… │
│ │ │ │ │ │ │ │
│ │ │ │ │ │ │ 803,072 │
│ │ │ │ │ │ │ (3.2 MB) │
├─────────┼────────┼────────────┼───────────┼─────────┼───────────┼────────────┤
│ Dense_1 │ Dense │ float32[1… │ float32[… │ 5130 │ 17940 │ bias: │
│ │ │ │ │ │ │ float32[1… │
│ │ │ │ │ │ │ kernel: │
│ │ │ │ │ │ │ float32[2… │
│ │ │ │ │ │ │ │
│ │ │ │ │ │ │ 2,570 │
│ │ │ │ │ │ │ (10.3 KB) │
├─────────┼────────┼────────────┼───────────┼─────────┼───────────┼────────────┤
│ │ │ │ │ │ Total │ 824,458 │
│ │ │ │ │ │ │ (3.3 MB) │
└─────────┴────────┴────────────┴───────────┴─────────┴───────────┴────────────┘
Total Parameters: 824,458 (3.3 MB)
4. Create a TrainState#
A common pattern in Flax is to create a single dataclass that represents the entire training state, including step number, parameters, and optimizer state.
Because this is such a common pattern, Flax provides the class
flax.training.train_state.TrainState
that serves most basic usecases.
!pip install -q clu
from clu import metrics
from flax.training import train_state # Useful dataclass to keep train state
from flax import struct # Flax dataclasses
import optax # Common loss functions and optimizers
We will be using the clu library for computing metrics. For more information on clu, refer to the repo and notebook.
@struct.dataclass
class Metrics(metrics.Collection):
accuracy: metrics.Accuracy
loss: metrics.Average.from_output('loss')
You can then subclass train_state.TrainState so that it also contains metrics. This has the advantage that we only need
to pass around a single argument to functions like train_step() (see below) to calculate the loss, update the parameters and compute the metrics all at once.
class TrainState(train_state.TrainState):
metrics: Metrics
def create_train_state(module, rng, learning_rate, momentum):
"""Creates an initial `TrainState`."""
params = module.init(rng, jnp.ones([1, 28, 28, 1]))['params'] # initialize parameters by passing a template image
tx = optax.sgd(learning_rate, momentum)
return TrainState.create(
apply_fn=module.apply, params=params, tx=tx,
metrics=Metrics.empty())
5. Training step#
A function that:
Evaluates the neural network given the parameters and a batch of input images with
TrainState.apply_fn(which contains theModule.applymethod (forward pass)).Computes the cross entropy loss, using the predefined
optax.softmax_cross_entropy_with_integer_labels(). Note that this function expects integer labels, so there is no need to convert labels to onehot encoding.Evaluates the gradient of the loss function using
jax.grad.Applies a pytree of gradients to the optimizer to update the model’s parameters.
Use JAX’s @jit
decorator to trace the entire train_step function and just-in-time compile
it with XLA into fused device operations
that run faster and more efficiently on hardware accelerators.
@jax.jit
def train_step(state, batch):
"""Train for a single step."""
def loss_fn(params):
logits = state.apply_fn({'params': params}, batch['image'])
loss = optax.softmax_cross_entropy_with_integer_labels(
logits=logits, labels=batch['label']).mean()
return loss
grad_fn = jax.grad(loss_fn)
grads = grad_fn(state.params)
state = state.apply_gradients(grads=grads)
return state
6. Metric computation#
Create a separate function for loss and accuracy metrics. Loss is calculated using the optax.softmax_cross_entropy_with_integer_labels function, while accuracy is calculated using clu.metrics.
@jax.jit
def compute_metrics(*, state, batch):
logits = state.apply_fn({'params': state.params}, batch['image'])
loss = optax.softmax_cross_entropy_with_integer_labels(
logits=logits, labels=batch['label']).mean()
metric_updates = state.metrics.single_from_model_output(
logits=logits, labels=batch['label'], loss=loss)
metrics = state.metrics.merge(metric_updates)
state = state.replace(metrics=metrics)
return state
7. Download data#
num_epochs = 10
batch_size = 32
train_ds, test_ds = get_datasets(num_epochs, batch_size)
8. Seed randomness#
Set the TF random seed to ensure dataset shuffling (with
tf.data.Dataset.shuffle) is reproducible.Get one PRNGKey and use it for parameter initialization. (Learn more about JAX PRNG design and PRNG chains.)
tf.random.set_seed(0)
init_rng = jax.random.key(0)
9. Initialize the TrainState#
Remember that the function create_train_state initializes the model parameters, optimizer and metrics
and puts them into the training state dataclass that is returned.
learning_rate = 0.01
momentum = 0.9
state = create_train_state(cnn, init_rng, learning_rate, momentum)
del init_rng # Must not be used anymore.
10. Train and evaluate#
Create a “shuffled” dataset by:
Repeating the dataset equal to the number of training epochs
Allocating a buffer of size 1024 (containing the first 1024 samples in the dataset) of which to randomly sample batches from
Everytime a sample is randomly drawn from the buffer, the next sample in the dataset is loaded into the buffer
Define a training loop that:
Randomly samples batches from the dataset.
Runs an optimization step for each training batch.
Computes the mean training metrics across each batch in an epoch.
Computes the metrics for the test set using the updated parameters.
Records the train and test metrics for visualization.
Once the training and testing is done after 10 epochs, the output should show that your model was able to achieve approximately 99% accuracy.
# since train_ds is replicated num_epochs times in get_datasets(), we divide by num_epochs
num_steps_per_epoch = train_ds.cardinality().numpy() // num_epochs
metrics_history = {'train_loss': [],
'train_accuracy': [],
'test_loss': [],
'test_accuracy': []}
for step,batch in enumerate(train_ds.as_numpy_iterator()):
# Run optimization steps over training batches and compute batch metrics
state = train_step(state, batch) # get updated train state (which contains the updated parameters)
state = compute_metrics(state=state, batch=batch) # aggregate batch metrics
if (step+1) % num_steps_per_epoch == 0: # one training epoch has passed
for metric,value in state.metrics.compute().items(): # compute metrics
metrics_history[f'train_{metric}'].append(value) # record metrics
state = state.replace(metrics=state.metrics.empty()) # reset train_metrics for next training epoch
# Compute metrics on the test set after each training epoch
test_state = state
for test_batch in test_ds.as_numpy_iterator():
test_state = compute_metrics(state=test_state, batch=test_batch)
for metric,value in test_state.metrics.compute().items():
metrics_history[f'test_{metric}'].append(value)
print(f"train epoch: {(step+1) // num_steps_per_epoch}, "
f"loss: {metrics_history['train_loss'][-1]}, "
f"accuracy: {metrics_history['train_accuracy'][-1] * 100}")
print(f"test epoch: {(step+1) // num_steps_per_epoch}, "
f"loss: {metrics_history['test_loss'][-1]}, "
f"accuracy: {metrics_history['test_accuracy'][-1] * 100}")
train epoch: 1, loss: 0.20290373265743256, accuracy: 93.87000274658203
test epoch: 1, loss: 0.07591685652732849, accuracy: 97.60617065429688
train epoch: 2, loss: 0.05760224163532257, accuracy: 98.28500366210938
test epoch: 2, loss: 0.050395529717206955, accuracy: 98.3974380493164
train epoch: 3, loss: 0.03897436335682869, accuracy: 98.83000183105469
test epoch: 3, loss: 0.04574578255414963, accuracy: 98.54767608642578
train epoch: 4, loss: 0.028721099719405174, accuracy: 99.15166473388672
test epoch: 4, loss: 0.035722777247428894, accuracy: 98.91827392578125
train epoch: 5, loss: 0.021948494017124176, accuracy: 99.37999725341797
test epoch: 5, loss: 0.035723842680454254, accuracy: 98.87820434570312
train epoch: 6, loss: 0.01705147698521614, accuracy: 99.54833221435547
test epoch: 6, loss: 0.03456473350524902, accuracy: 98.96835327148438
train epoch: 7, loss: 0.014007646590471268, accuracy: 99.6116714477539
test epoch: 7, loss: 0.04089202359318733, accuracy: 98.7880630493164
train epoch: 8, loss: 0.011265480890870094, accuracy: 99.73333740234375
test epoch: 8, loss: 0.03337760642170906, accuracy: 98.93830108642578
train epoch: 9, loss: 0.00918484665453434, accuracy: 99.78334045410156
test epoch: 9, loss: 0.034478139132261276, accuracy: 98.96835327148438
train epoch: 10, loss: 0.007260234095156193, accuracy: 99.84166717529297
test epoch: 10, loss: 0.032822880893945694, accuracy: 99.07852172851562
11. Visualize metrics#
import matplotlib.pyplot as plt # Visualization
# Plot loss and accuracy in subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
ax1.set_title('Loss')
ax2.set_title('Accuracy')
for dataset in ('train','test'):
ax1.plot(metrics_history[f'{dataset}_loss'], label=f'{dataset}_loss')
ax2.plot(metrics_history[f'{dataset}_accuracy'], label=f'{dataset}_accuracy')
ax1.legend()
ax2.legend()
plt.show()
plt.clf()
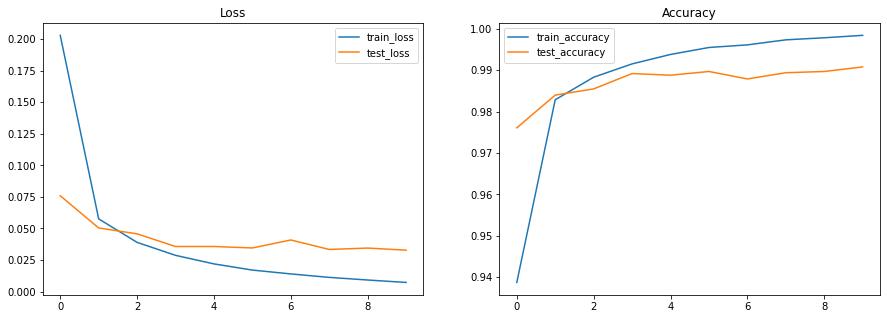
<Figure size 600x400 with 0 Axes>
12. Perform inference on test set#
Define a jitted inference function pred_step. Use the learned parameters to do model inference on the test set and visualize the images and their corresponding predicted labels.
@jax.jit
def pred_step(state, batch):
logits = state.apply_fn({'params': state.params}, test_batch['image'])
return logits.argmax(axis=1)
test_batch = test_ds.as_numpy_iterator().next()
pred = pred_step(state, test_batch)
fig, axs = plt.subplots(5, 5, figsize=(12, 12))
for i, ax in enumerate(axs.flatten()):
ax.imshow(test_batch['image'][i, ..., 0], cmap='gray')
ax.set_title(f"label={pred[i]}")
ax.axis('off')

Congratulations! You made it to the end of the annotated MNIST example. You can revisit the same example, but structured differently as a couple of Python modules, test modules, config files, another Colab, and documentation in Flax’s Git repo:


